Geodesic domes are a fascinating attempt at a Fullerian idealization of human habitant and other use buildings. Approzimating a sphere, their "claim to fame" is that they have the smallest surface area to volume ratio, making them theoretically the most efficient building shape to heat or cool (condition). There are also idealistic mentions of prefabricability and standardization for efficiencies of manufacture and placement on site. Before truly questioning these assumptions, I used to accept them as dogma, and try to design ways of, for instance, fully utilizing the space inside the dome, to add my small potential contribution to the body of work. Then one day, I started doing some random searching and interesting reading on the topic. I will briefly recount the difficulties and disappointments encountered by people who really believed in geodesic living. These are the real life problems with bringing this ideal to reality. First, even though one could imagine a world in which all the lumber at the local yard is conveniently cut to lengths and angles required in geodesic construction, in the end their construction is very wasteful of materials. A dome (of any size) requires several similar but not identical lengths of lumber (or other structural material), and also several different sized polygonal panels. The panels could only be made efficiently if they were molded in some way out of raw material - their shapes cannot be cut from sheets without great wastage of material. Contrast this with a rectangular box built to multiples of some standard length (like four feet, or some metric equivalent). There might be so little scrap that fresh material must be cut just to make the occasional brace or fire break. This is because a plane material (like a sheet of plywood) or a solid (like a chunk of lumber) can be most efficiently divided up into rectangles - especially if its production generates parallel sides to start with. While hexagons will fill a plane surface with 100% efficiency, at the edges you get a sixty degree zig-zag pattern that must be accomodated, wasted, or reprocessed. Pentagons are just plain wasteful to make. Second, all the complex angles and joints are prone to leakage. Again, compared with a simple gabled roof on a rectangular building, which basically only has one vulnerable seam (the ridgeline), or seven if we also count the eaves and gable ends, a dome has literally hundreds of joined seams which must all be weatherproof. Third, a sphere, or sphere-like shape has terrible acoustics. The more "open" the internal space is, and modern building and living trends have moved very much towards this style, the more this acoustic nightmare is let loose. These acoustics tend to magnify and propagate any sounds generated inside the building, rather than damping and dissipating them. They also create a rather claustrophobic "sense of space" at certain focal points in the building. Fourth, and perhaps not such a big issue if we imagine our new world to have many standardized products with which to build domes, is the issue of "penetrations" - things that make holes in the "wall" or "roof" of our buildings to make them usable and/or livable. Windows, doors and chimneys all create new problems, owing to the lack of conventional vertical or horizontal planes over most of the dome structure. The same sort of problem is encountered in the horizontal plane, where the outer walls of the dome keep curving in on the living space. Scale is what matters here, along with the readiness of people to adopt furniture of varying shapes. As long as the straight lines are long enough to accomodate a typical couch or bed, it wouldn't really matter much. hanging art would be frustrating as well, since very few, if any, of the dome wall sections would be convenienty vertical. These problems cannot be wished away by idealistic statements about conditioning efficiency or modular construction materials, they are simple physical realities. Disappointing realities, to the dome enthusiasts throughout the world who have attempted to experiment and promote the concept. But what of my reason for writing this? After all, everything I have just said could be discovered or worked out by anyone with piece of paper and a computer connected to the "internets." The problem is in the basic assumption! The idea that the dome creates the most energy efficient enclosed space ignores some fundamental realities of what they are to be used for. If all we are doing is enclosing some amorphous matter, like a gas, or a few tons of corn, or mothballs, the efficiency dogma holds true - we get the most volume for the amount of materials used in the outer surface, and the greatest conditioning efficiency. But, people are not amorphous. A lot of the time, they occupy a space that is about six feet high by perhaps a square foot or two in area. Such things cannot be "stored" efficiently in an enclosure that has curved edges. Even in repose, there are vertical requirements - room to stand up out of a chair (and even seated, the critter is four or so feet high), space to get up out of bed, and so on. So the dome creates a lot of "difficult to utilize" nooks and crannies around its perimeter. Buckminster Fuller attempted to address this to an extent by designing a system of drawers that could rotate in and out of this "difficult" space. But even allowing for this cumbersome storage (you still can't hang dresses or suits or coats there), and beds and chairs tucked into the curved overhangs, there is only so much need for this space. For people to comfortably and efficiently use a living space, it needs to be around seven to eight feet high, and have vertical walls. It can be higher, at a cost of efficiency - conditioning "unused" volume - but often at a gain in pleasantness of use. As it turns out, if you carve the inside of a dome into such spaces - "people height" with vertical inner walls - the dome ends up having a greater surface area through which to lose or gain heat that a simple, well proportioned rectangular box! This means that unless all that weird curved space can be truly and usefully allocated to living needs, the energy cost of maintaining the structure will be higher than a rectangular structure providing the same living space. 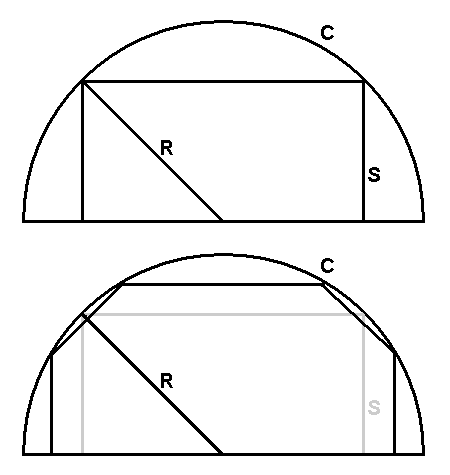 Figure 1 shows how this happens. Both buildings are shown in cross section (the dome floor plan is round, of course, and the "rectangle" is square). The rectangle has a flat roof. If a pitched roof is added, the insulation is still placed at the same conditioned/unconditioned boundary, at the flat ceiling. The "useful volume" is the same in both cases. S = R * sqr(2)/2 or R = S * sqr(2) ... (for conversion between R and S, assumes drawn R is at 45 degrees) Ab = ((2 * S)^2) + 4 * (S * 2 * S) ... (area of roof plus four sides)
Ad = 2 * π * R^2 ... (from area of sphere)
Ab is to Ad as 12 is to 4π - the dome's external area is greater than that of the box for the same useful interior space. The rectangle is even more efficient if it steals a page from the dome, and inflicts the roofline on two sides of the living space. Its cross-section closer approximates the "ideal" sphere, without creating unnecessary wasted conditioned space. Whether this works depends on where the ceiling cut offs are - too much encroachment creates the same problem as the dome's curved walls - wasted space with poor headroom. Just the right amount is not missed, as it would be over such second floor (for example) installations as commodes, dressers and Fullerian "short" closets. When it comes down to it, sadly for the idealists, the dome's horrendous contruction difficulties don't pay off with greater efficiency in use, either of space utilization or energy consumption. 1/1/07 (after notes made a year or two ago) © Huw Powell
|